Two Probability Exercises

Exercise 1

A and B are playing a game (e.g. table tennis), which comprises 5 sets; whoever firstly wins 3 sets is the winner. We make two assumptions: (a) The probability that A wins a set is $p$ ($0<p<1$), and the probability that B wins a set is $1-p$; (b) the 5 sets are independent. What is the probability that A wins the game?

Solution. Let $X$ be the number of sets that A wins in a game. Then, $X$ has the binomial distribution $B(5,p)$. The probability that A wins the game is

$$\begin{array}{rl}\text{Pr}(X\ge 3)& =\sum _{i=3}^5(\genfrac{}{}{0ex}{}{5}{i})p^i(1-p{)}^{5-i}\\ & =6p^5-15p^4+10p^3.\end{array}$$

I asked myself this question: Is this winning probability $\text{Pr}(X\ge 3)$ greater or less than $p$? To find out the answer to this question, I plot the winning probability against $p$ and the 45-degree line:

n_out_of_2n_minus_1 <- function(n, p)
{m <-  2*n - 1
 s <- 0
 for(j in n:m) {
   s <- s + choose(m, j) * p^j * (1-p)^(m-j)
 }
 return(s)
}

x <- seq(0.001, 0.999, length.out = 1000)
y <- n_out_of_2n_minus_1(n = 3, p = x)

plot(x, y, type = 'l', xlab = 'p', ylab = 'Winning probability')
abline(a = 0, b = 1, col = 'red', lty = 2)
abline(v = 0.5, col = 'red', lty = 2)  

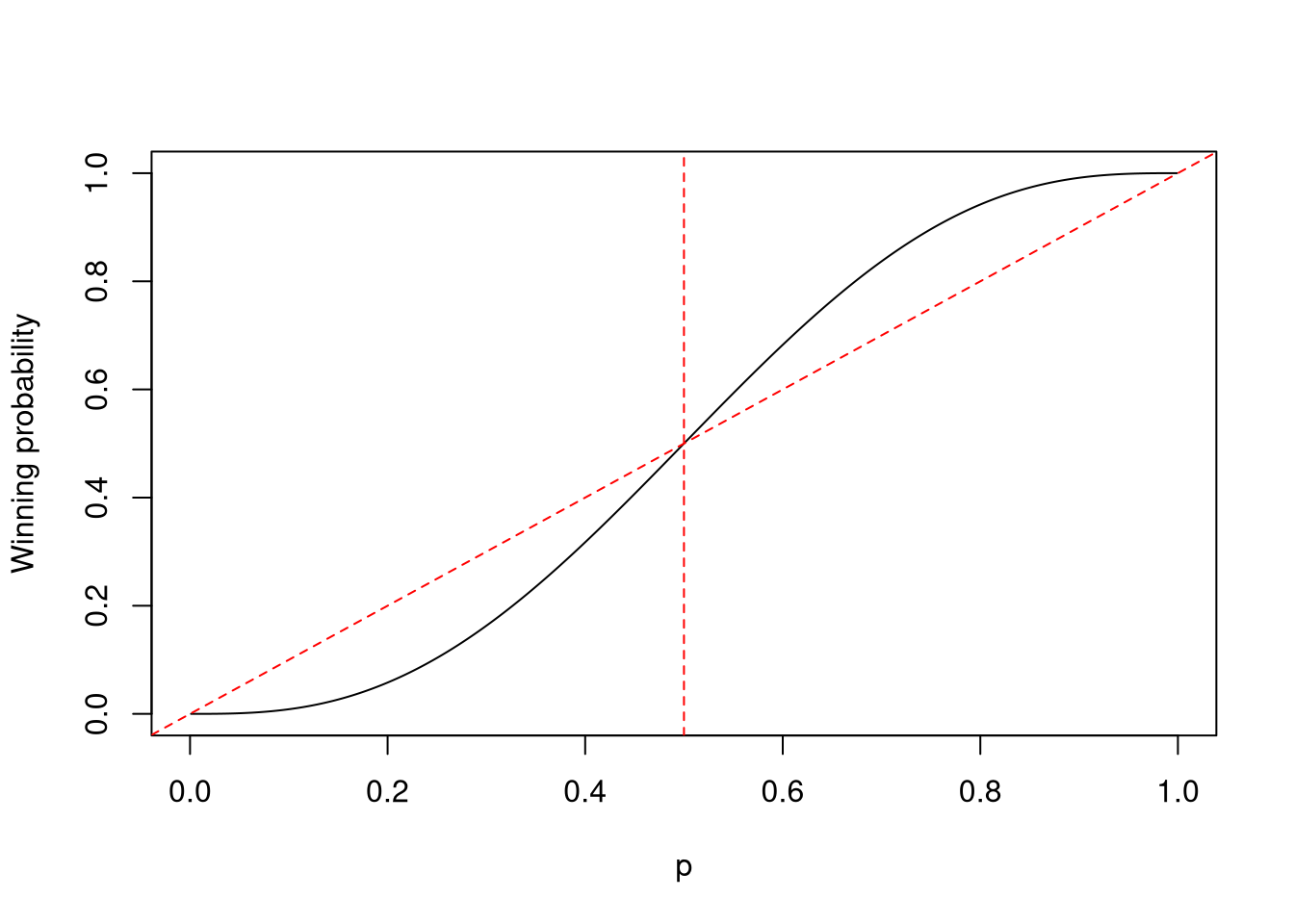
The above plot shows that: the winning probability is

• $>p$, if $p>0.5$,
• $=p$, if $p=0.5$,
• $<p$, if $p<0.5$.

This is interesting!

Exercise 2

Two gamblers, A and B, are playing a game of 13 rounds. The rule is: Whoever firstly wins 7 rounds will collect the entire prize. All the rounds are independent; the probability that A wins a round is $p$ ($0<p<1$), and the probability that B wins a round is $1-p$. The following situation is of interest: After 9 rounds, A has won 5 rounds and B has won 4 rounds. However, for some reason, they must stop the game here. How do they divide the prize?

So, here I am talking about the famous problem of points (AKA division of the stakes).This wikipedia article provides a solution. The key is to figure out A’s winning probability if they carry on the game until round 13. Now, I want to find A’s winning probability with a Markov chain approach.

The state space is $5,6,7+$ — each state is a count of how many rounds that A has won. The initial distribution is:

$$\left(\begin{array}{lll}5& 6& 7+\\ 1& 0& 0\end{array}\right).$$

The transition matrix is

$$\mathit{P}=\left[\begin{array}{ccc}1-p& p& 0\\ 0& 1-p& p\\ 0& 0& 1\end{array}\right]$$

Note that if they carry on the game A’s winning probability is given by

$$[1,0,0]{\mathit{P}}^4{\mathit{e}}_3,$$

where ${\mathit{e}}_3^T=[0,0,1]$. It’s easy to find

$${\mathit{P}}^2=\left[\begin{array}{ccc}(1-p{)}^2& 2p(1-p)& p^2\\ 0& (1-p{)}^2& 2p-p^2\\ 0& 0& 1\end{array}\right]$$

Therefore,

$$[1,0,0]{\mathit{P}}^4{\mathit{e}}_3=[(1-p{)}^2,2p(1-p),p^2]\left[\begin{array}{c}{p}^2\\ 2p-p^2\\ 1\end{array}\right],$$

which is equal to $3p^4-8p^3+6p^2$.