Triangles on the Unit Circle

Introduction

We consider the following three problems: For any random triangles on the unit circle,

1. which triangle has the largest perimeter?
2. which triangle has the largest area?
3. what’s the average area of the triangles?

Solution to the problem 1

Denote a triangle by $ABC$, then

$$\begin{array}{r}\frac{a}{2}=\frac{BC}{2}=\sin \frac{\beta }{2},\\ \frac{b}{2}=\frac{CA}{2}=\sin \frac{\gamma }{2},\\ \frac{c}{2}=\frac{AB}{2}=\sin \frac{\alpha }{2}.\end{array}$$

Thus,

$$s=\frac{a+b+c}{2}=\sin \frac{\alpha }{2}+\sin \frac{\beta }{2}+\sin \frac{\gamma }{2},$$

where $\alpha +\beta +\gamma =2\pi .$ Now, we formulate the problem as: Find $\alpha$, $\beta$ and $\gamma$ such that $s$ attains its maximum. Define

$$L(\alpha ,\beta ,\gamma ;\lambda )=\sin \frac{\alpha }{2}+\sin \frac{\beta }{2}+\sin \frac{\gamma }{2}+\lambda (\alpha +\beta +\gamma -2\pi ).$$

Taking partial differentials, and we solve

$$\begin{array}{r}\frac{\partial L}{\partial \alpha }=\frac{\cos (\alpha /2)}{2}+\lambda =0\\ \frac{\partial L}{\partial \beta }=\frac{\cos (\beta /2)}{2}+\lambda =0\\ \frac{\partial L}{\partial \gamma }=\frac{\cos (\gamma /2)}{2}+\lambda =0\\ \frac{\partial L}{\partial \lambda }=\alpha +\beta +\gamma -2\pi =0\end{array}$$

We get

$$\alpha =\beta =\gamma =\frac{2\pi }{3}.$$

The Hessian matrix is

$$H=\left[\begin{array}{cccc}-\frac{\sin \frac{\alpha }{2}}{4}& 0& 0& 1\\ 0& -\frac{\sin \frac{\beta }{2}}{4}& 0& 1\\ 0& 0& -\frac{\sin \frac{\gamma }{2}}{4}& 1\\ 1& 1& 1& 0\end{array}\right].$$

It's easy to show that $H$ is negative definite when $\alpha =\beta =\gamma =\frac{2\pi }{3}.$ So the triangle that has the largest perimeter is an **equilateral triangle** on the unit circle.

Solution to problems 2 and 3

It’s kind of difficult to have analytic solutions to problems 2 and 3. So we resort to Monte Carlo simulation.

• We can think that coordinates of $A$, $B$ and $C$ are $(\cos \alpha ,\sin \alpha )$, $(\cos \beta ,\sin \beta )$, and $(\cos \gamma ,\sin \gamma )$, respectively, where $0\le \alpha ,\beta ,\gamma \le 2\pi .$

• The lengths of the three edges are

$$\begin{array}{r}a=BC=\sqrt{(\cos \beta -\cos \gamma {)}^2+(\sin \beta -\sin \gamma {)}^2}\\ b=CA=\sqrt{(\cos \alpha -\cos \gamma {)}^2+(\sin \alpha -\sin \gamma {)}^2}\\ c=AB=\sqrt{(\cos \alpha -\cos \beta {)}^2+(\sin \alpha -\sin \beta {)}^2}\end{array}$$

• The area is

$$\sqrt{s(s-a)(s-b)(s-c)},$$

where

$$s=\frac{a+b+c}{2}.$$

R code:

d <- function(x, y) sqrt((cos(x) - cos(y))^2 + (sin(x) - sin(y))^2)

a_simu <- function()
{rand_nbrs <- runif(3, min = 0, max = 2 * pi)
 a <- d(rand_nbrs[2], rand_nbrs[3])
 b <- d(rand_nbrs[1], rand_nbrs[3])
 c <- d(rand_nbrs[1], rand_nbrs[2])
 s <- (a + b + c) / 2
 A <- sqrt(s * (s-a) * (s-b) * (s-c))
}

set.seed(12345)
N <- 1e4
simu_res <- replicate(n = N, a_simu(), simplify = TRUE)


(summary(simu_res))

##      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
## 0.0000005 0.1348081 0.3928584 0.4770273 0.7711802 1.2989897

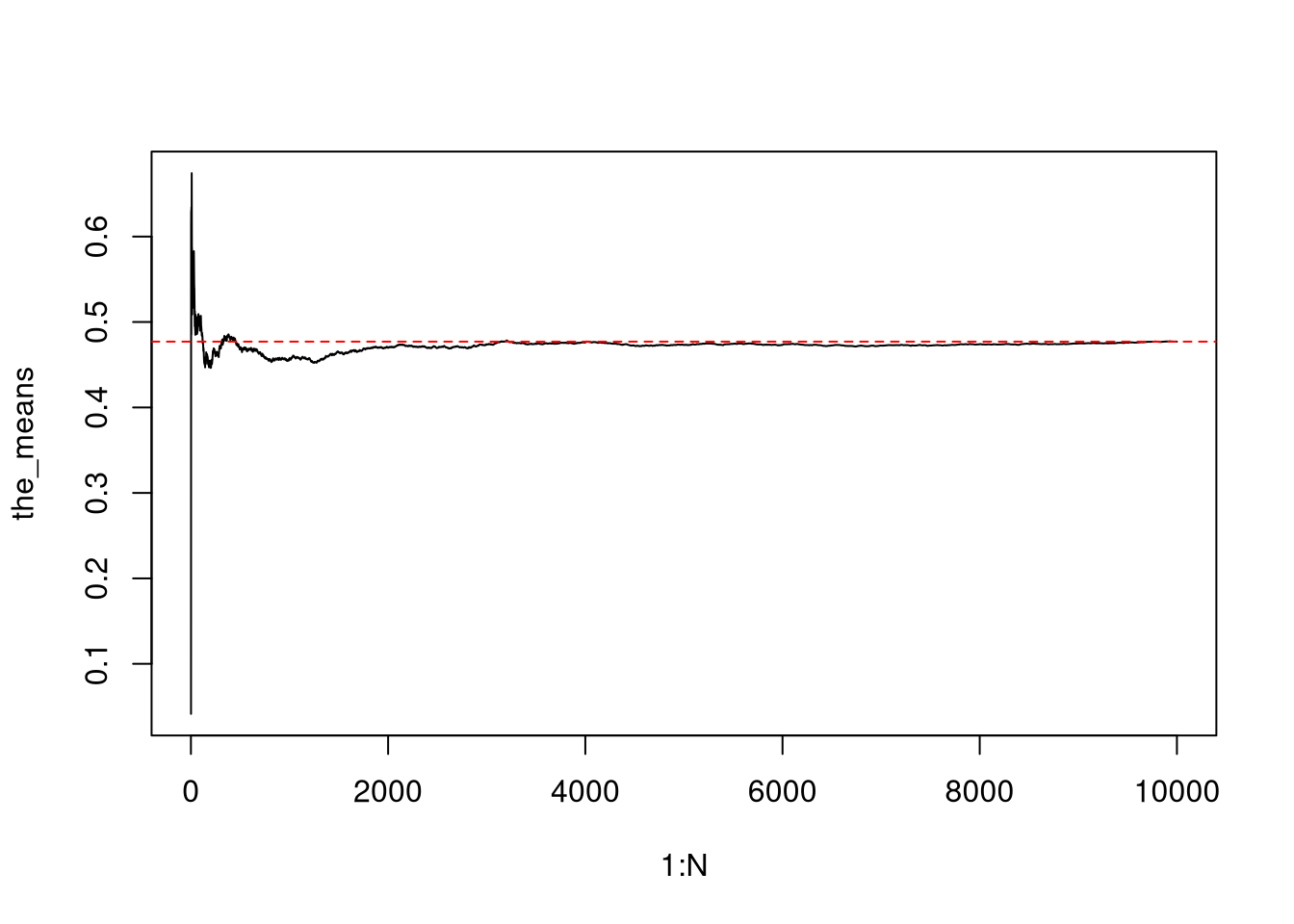
the_means <- cumsum(simu_res) / (1:N)
(the_means[N])

## [1] 0.4770273

plot(1:N, the_means, type = 'l')
abline(a = the_means[N], b = 0, lty = 2, col = 'red')

Note that 1.2989897 is very close to $\frac{3\sqrt{3}}{4}$, which is the area of an equilateral triangle on the unit circle. Thus, we have evidence to say that the the largest area is attained by an equilateral triangle on the unit circle.

Also note that 0.4770273 is close to $\frac{3}{2\pi }$, which is the answer that we seek for the problem 3—according to this web site.