Resolving a Problem from Professor Strang

Introduction

Renowned MIT professor Gilbert Strang gave a talk, which can be accessed here. In the talk, he presented the following problem: If a triangle is chosen randomly, what is the probability that it is acute (i.e., all angles are less than 90 degrees)? Professor Strang provided two solutions to this problem.

In this note, I will resolve the problem by providing three solutions. Solution 1 is taken from Professor Strang’s talk; Solution 2 is inspired by Solution 1; Solution 3 utilizes the Monte Carlo method.

Three Solutions

In Solutions 1 and 2, $x$, $y$ and $z$ denote three angles of a triangle.

Solution 1 (from Professor Strang)

The problem can be formulated as follows: If

$$ x+y+z = 180,\ \hbox{and}\ 0 < x,\ y,\ z < 180, $$

what is the probability that

$$ 0 < x,\ y,\ z < 90? $$

We can have a picture of the above formulation

Using the above picture, it’s easy for us to find the probability is $1/4$.

Solution 2

Inspired by Solution 1, we can reformulate the problem as: If

$$ 0 < x,\ y < 180\ \hbox{and}\ x+y < 180, $$

what is the probability that

$$ x+y< 90? $$

The picture of this formulation is

From this picture, we can easily figure out the probability is $1/4$.

Solution 3: Monte Carlo method

Note this fact: For any a triangle in the plane, we can find its circumscribed circle. Next, we move the circumcircle such that its centre is the origin. Finally, we can find the one and the only one triangle on the unit circle that is similar to the original triangle.

Based on the above fact, for Professor Strang’s problem we only need to consider triangles on the unit circle.

We use Monte Carlo method. The major steps are:

1. Randomly generate three points on the unit circle.
2. Find the lengths of the three sides of the triangle.
3. Using the cosine law to find cosine values of the three angles, and test if all the cosine values are non-negative.
4. Repeat Steps 1–3 N (e.g. N = 10,000) times.

R code:

distance <- function(x, y)
{AB <- sqrt((x[1] - x[2])^2 + (y[1] - y[2])^2)
 AC <- sqrt((x[1] - x[3])^2 + (y[1] - y[3])^2)
 BC <- sqrt((x[2] - x[3])^2 + (y[2] - y[3])^2)
 list(AB, AC, BC)
}

a_simu <- function()
{x <- runif(3, min = -1, max = 1)
 the_signs <- 2 * rbinom(3, size = 1, prob = 0.5) - 1
 y <- sqrt(1 - x^2) * the_signs
 d_list <- distance(x, y)
 a <- d_list[[3]]
 b <- d_list[[2]]
 c <- d_list[[1]]
 cosA <- (b^2 + c^2 - a^2) / (2 * b * c)
 cosB <- (a^2 + c^2 - b^2) / (2 * a * c)
 cosC <- (a^2 + b^2 - c^2) / (2 * a * b)
 m <- min(c(cosA, cosB, cosC))
 return(m >= 0)
}

set.seed(12345678)
N <- 10000
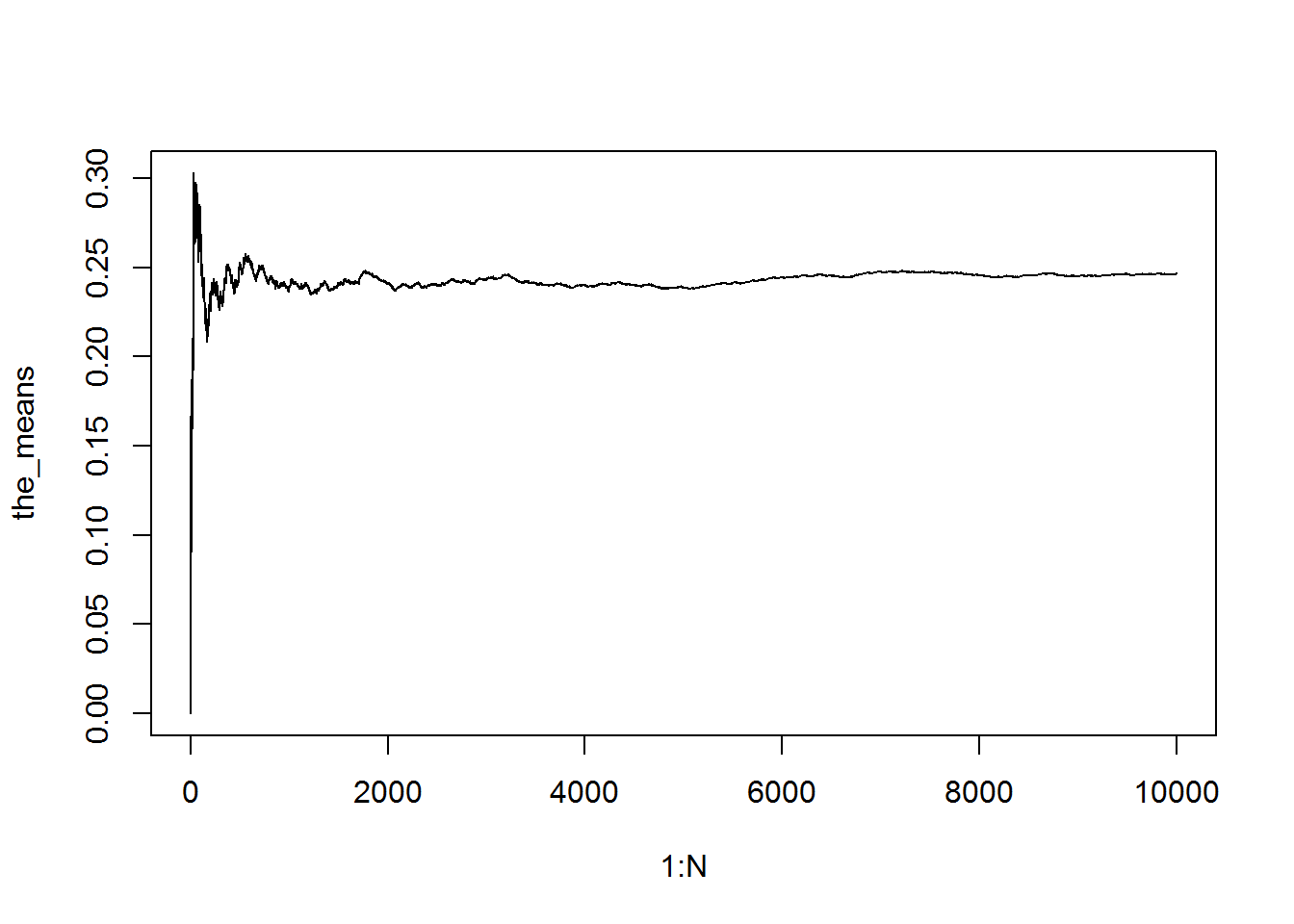
the_simu_re <- replicate(n = N, expr = a_simu())
the_means <- cumsum(the_simu_re) / (1:N)
(the_means[N])

## [1] 0.2464

plot(1:N, the_means, type = 'l')

Concluding remarks

Not only can Solutions 1 and 2 give the answer, but they also indicate that: if we randomly pick up a triangle, then the probability that it’s a right triangle is 0.