Finding the Radius of the Brown Circle

Introduction

Peter’s post (the link) caught my attention. He used a brute force method to solve the following problem, which is originally from this tweet.

NB: The above picture was created by Peter.

I will try out the problem, following a two-step process:

1. Set up equations.
2. Solve the equations.

Solving The Problem

Step 1

The equation for the brown circle can be written as

$$ (x-x_0)^2 + (y-y_0)^2 = r^2, $$

where point $(x_0, y_0)$ is the center $C$ and $r$ is the radius of the circle, respectively. Since $y$-axis is a tangent line to the circle,

$$ x_0 = r. $$

Given that the purple and brown circles are tangent to each other, we have

$$ \sqrt{(x_0-0)^2+(y_0-0)^2}=\sqrt{r^2+y_0^2}=1-r, $$

from which it follows that

$$ y_0=\sqrt{(1-r)^2-r^2}=\sqrt{1-2r}. $$

Based on the above analysis, we now know that the center of the brown circle (i.e. point $C$) is: $(r, \sqrt{1-2r})$. Suppose that the brown circle and the red parabola intersect at point $A$ with coordinates $(u, \sqrt{u})$. As preparation, we find derivative of $y = \sqrt{x}$

$$ y^{\prime} = \frac{1}{2\sqrt{x}}, $$

and

$$ y^{\prime}|_{x = u} = \frac{1}{2\sqrt{u}}. $$

If we connect points $C$ and $A$, then we have two facts

• the resulted line should have tangent being equal to

$$ \frac{-1}{\frac{1}{2\sqrt{u}}}=-2\sqrt{u}; $$

• the distance between $C$ and $A$ should be $r$.

Using the above two facts, we have the following equations

$$ \left\{ \begin{array}{l} \frac{\sqrt{1-2r}-\sqrt{u}}{r-u}=-2\sqrt{u}\\ (r-u)^2 +(\sqrt{1-2r}-\sqrt{u})^2=r^2 \end{array} \right. $$

We can slightly simplify the above two equations by letting

$$ d = u - r, $$

and we have

$$ \left\{ \begin{array}{l} \frac{\sqrt{1-2r}-\sqrt{d+r}}{d}=2\sqrt{d+r}\\ d^2 +(\sqrt{1-2r}-\sqrt{d+r})^2=r^2 \end{array} \right. $$

which imply the **key equation** \begin{equation} 1 + 4(d+r)=\frac{r^2}{d^2}. \end{equation} From the key equation, we can find that

$$ r = 4d^2+d. $$

At this point, we have set up the equations:

$$ \left\{ \begin{array}{l} r = 4d^2+d\\ d^2 +(\sqrt{1-2r}-\sqrt{d+r})^2=r^2 \end{array} \right. $$

Step 2

We solve the above two equations with the following R code.

library(rootSolve) # for uniroot()

d_func <- function(d)
{r <- 4*d^2 + d
 d^2 + (sqrt(1 - 2*r) - sqrt(d + r))^2 - r^2
}

curve(d_func, 0.0, 0.15)
abline(a = 0, b = 0, col = 'red')

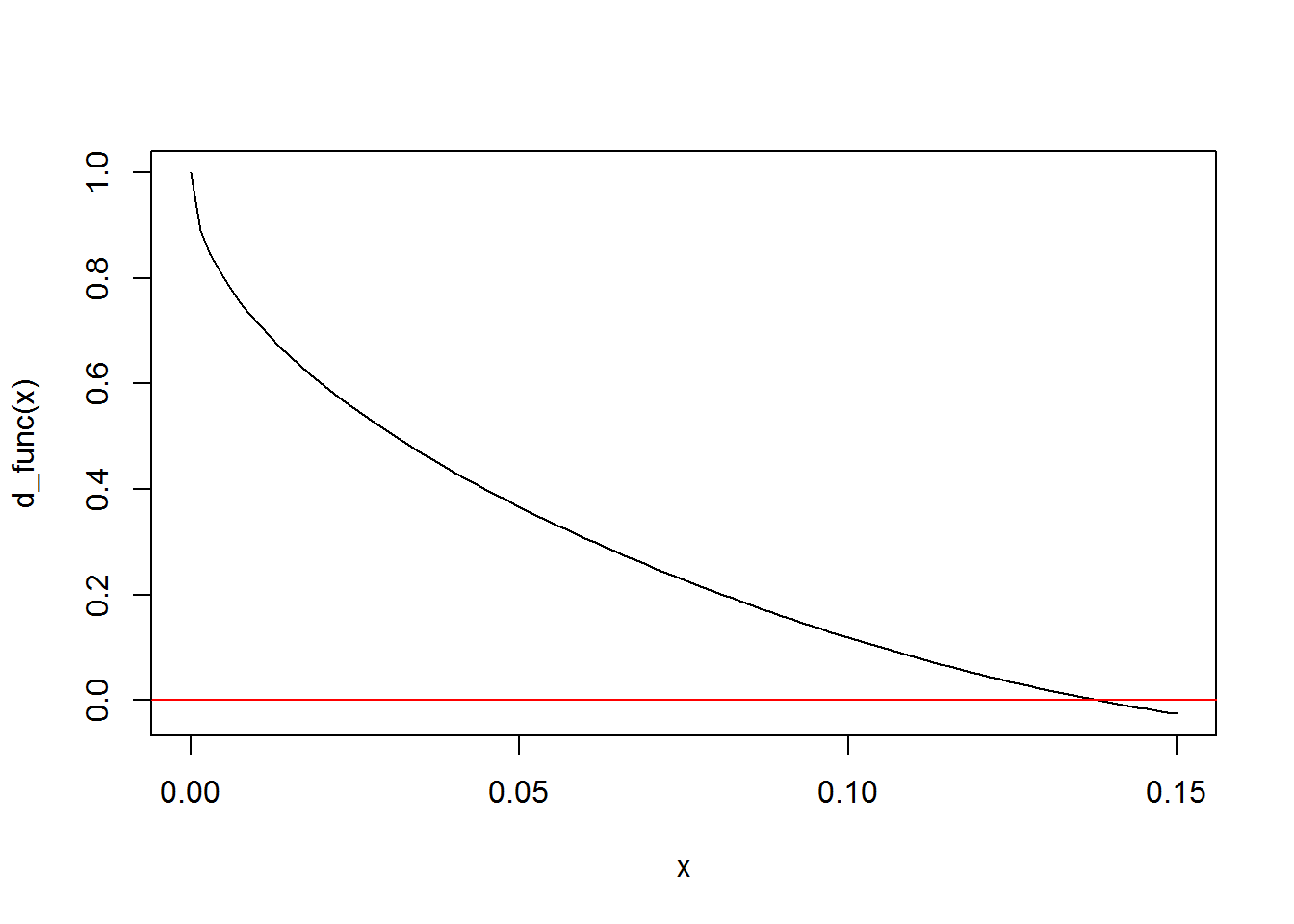
the_root <- uniroot(d_func, c(0.0, 0.15), tol = 1e-8)$root
(r <- 4 * the_root^2 + the_root)

## [1] 0.2138418

NB: I firstly had tried curve(d_func, 0.0, 1.0), and then I knew $d$ should be in the interval from 0 to 0.15.