Introduction

This post (https://qr.ae/prO6WG) on Quora asks for a proof that

$$ \cos(\sin(x)) > \sin(\cos(x)), \ \hbox{for}\ x\in R. $$

Senia Sheydvasser gives a solution. In this post, I will give a better solution.

A solution

We define that

$$ f(x) = \cos(\sin(x)) - \sin(\cos(x)), \ \hbox{for}\ x\in R. $$

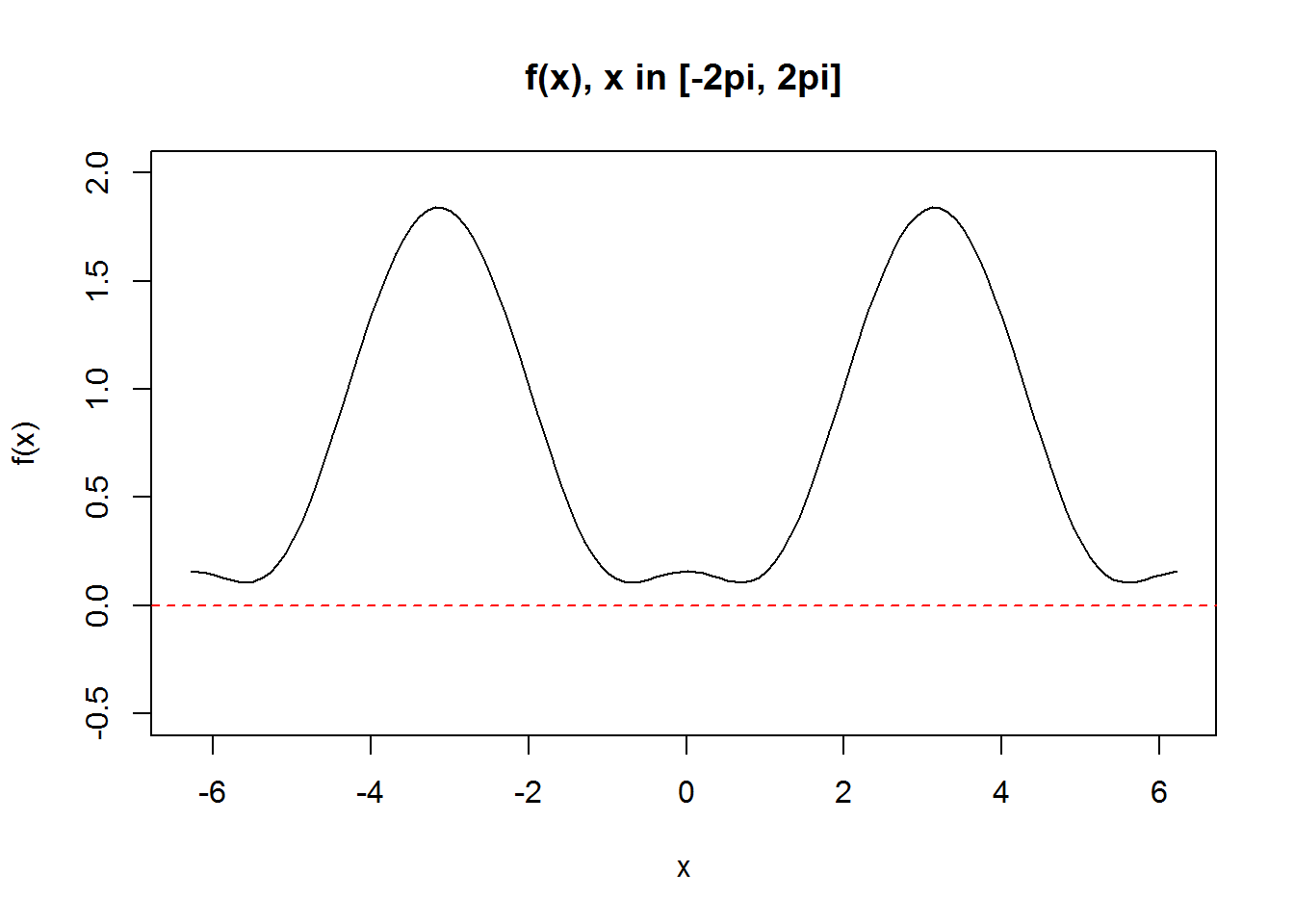
So we want to prove that

$$ f(x) > 0, \ \hbox{for}\ x\in R. $$

Proof:

It’s obvious that $f(x)$ is a periodic function and $2\pi$ is its period. Thus, we only need to show that

$$ f(x) > 0, \ \hbox{for}\ x\in [-\pi, \pi]. $$

Since $g(x) = \cos(x)$ is even and $h(x) = \sin(x)$ is odd, $f(x)$ is even. Thus, we only need to show that

$$ f(x) > 0, \ \hbox{for}\ x\in [0, \pi]. $$

Notice that

$$ \cos(\sin(x)) > 0, \ \hbox{for}\ x\in R, $$

and

$$ -\sin(\cos(x)) \ge 0, \ \hbox{for}\ x\in [\pi/2, \pi]. $$

We thus only need to show that

$$ f(x) > 0, \ \hbox{for}\ x\in [0, \pi/2], $$

which is true because when $x\in [0, \pi/2]$

$$ \frac{\pi}{2}\ge \frac{\pi}{2} - \sin(x) > \cos(x) \ge 0 $$

and $h(x) = \sin(x)$ is an increasing function, and

$$ f(x) = \sin(\pi/2- \sin(x)) - \sin(\cos(x)) > 0. $$

Some people may ask this question: Why is it true that

$$ \frac{\pi}{2} - \sin(x) > \cos(x)? $$

Here is the answer:

$$ \sin(x)+\cos(x)=\sqrt{2}\sin(x + \pi/4)\le \sqrt{2}; $$

thus,

$$ \begin{array}{cl} & (\frac{\pi}{2}-\sin(x)) - \cos(x)\\ = & \frac{\pi}{2}-(\sin(x) + \cos(x))\\ \ge & \frac{\pi}{2} -\sqrt{2}\\ > & 0. \end{array} $$

At this point, the proof is completed.

Appendix: R code for plotting $f(x)$

x <- seq(-2*pi, 2*pi, by = 0.1)
y <- cos(sin(x)) - sin(cos(x))
plot(x, y, type = 'l', ylim = c(-0.5, 2),
     main = "f(x), x in [-2pi, 2pi]",
     ylab = "f(x)")
abline(a = 0, b = 0, col = 'red', lty = 2)